|
|
||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
Arquitectura e Ciência – António Rodrigues São parcos os dados biográficos sobre o Arquitecto António Rodrigues (c.1520-1590). Deve ter iniciado o seu contacto com o mundo da construção no estaleiro de Tomar, sendo um dos moços da estribeira que Dom João III utilizava para trazer informação sobre as obras 1 , e completado a sua formação em Itália. Certo é que chegou a 1º Cavaleiro fidalgo da casa de el-rei e ascendeu a mestre das obras reais, com Dom Sebastião, em 1565, sucedendo a Miguel de Arruda, e a mestre de obras das fortificações, em 1575, após a morte de Afonso Álvares, tendo acumulado ambos os cargos durante 15 anos facto que constitui caso único no país. Deve-se a Rafael Moreira a reposição desta personagem singular na ribalta da história da arquitectura portuguesa, ao atribuir-lhe um projecto de um Tratado de Arquitectura (com uma versão preliminar de 1576 e outra, visando o prelo, de 1579, ambas incompletas) 2 que serviria de suporte à “Lição de Arquitectura Militar” de que foi responsável na Escola de Moços Fidalgos do Paço da Ribeira, bem como a autoria, documentalmente comprovada, da Igreja de Santa Maria da Graça de Setúbal (actual Sé), e, por confronto estilístico, da Capela das Onze Mil Virgens, em Alcácer do Sal 3 , construída adossada à Igreja do Convento de Stº António para jazigo de Dom Pedro de Mascarenhas 4 .
Esta arquitectura, onde o material e a cuidada administração da luz assumem particular relevância ‒ dir-se-ia quase minimal, ao tempo ‒ encontrará eco no famoso estilo desornamentado espanhol de raiz herreriana, abrindo portas ao denominado estilo chão, que conheceu grande fortuna entre nós, e que se caracteriza por aliar à singeleza de recursos uma sólida estruturação espacial escudada na pureza da geometria. Na obra de António Rodrigues, particularmente, a omnipresença da geometria, sempre associada ao número, é uma condição essencial para a caracterização da sua arquitectura. É insuspeitável também, por outro lado, o sentido cósmico desta estreita ligação, e de como, em acordo com o neoplatonismo, cada obra se constrói como um perfeito microcosmos para ser a representação do macrocosmos matematicamente ordenado. Em qualquer das suas obras se detecta a existência de variadíssimas formas e construções que povoam o seus “Livros” de Geometria, “Trigonometria” e de Perspectiva, que reencontramos disseminadas pelos tratados que inspiraram o seu, e que, à falta dos livros sequentes, desconhecidos ou nunca completados, se materializaram na conformação dos espaços arquitectónicos que produziu. |
||||||||||||||||||||||||||||||||||||||||
| Capela das Onze Mil virgens | ||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
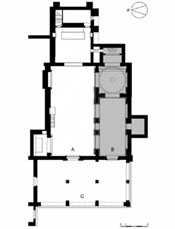
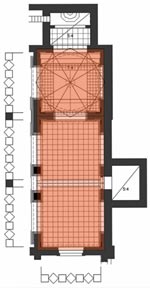
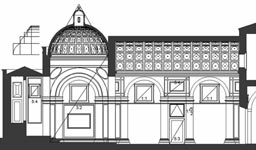
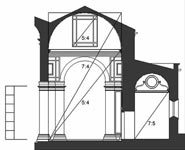
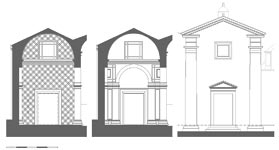
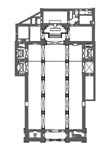
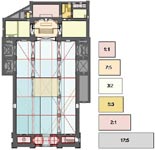
| Capela das Onze Mil Virgens: planta, corte longitudinal e cortes transversais (Clique nas imagens para as ampliar) |
||||||||||||||||||||||||||||||||||||||||
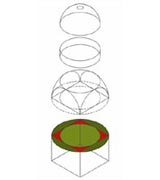
A Capela das Onze Mil Virgens reflecte na sua organização planimétrica a estrutura do mítico Templo de Salomão. A nave, um duplo quadrado, antecede o espaço do sepulcro, um quadrado simples, tal como no arquétipo. À nave adossa-se, lateralmente, a sacristia; no terminus do eixo longitudinal do templo situa-se a capela-mor, onde se guardam as relíquias das Virgens trazidas por Dom Pedro aquando da sua passagem por Colónia como Embaixador de Portugal junto do Imperador Carlos V. Ambas os espaços são de proporção sexquiquarta (hua proposição de hum quadrado e hu quarto) 5 , assim como a secção transversal da nave. A modulação geral do templo faz uso de uma geometria ad quadratum que se evidencia no espaço dominante, o mausoléu, uma caixa espacial cúbica coroada por uma cúpula semiesférica assente sobre pendentes (triângulos esféricos que, por sua vez, circunscrevem óculos circulares) onde o jogo entre o quadrado e o círculo espelha, com intencionalidade, a relação entre a terra, que recebe as sepulturas, e o céu, para o qual se elevam as almas. E que céu esse! Uma cúpula absolutamente notável pela sua expressão formal, precisão da estereotomia e pelo material. Divide-se em 24 semi-meridianos e 7 paralelos, números de evidente tradução cósmica, visando simbolizar através da geometria, expressamente afirmada, a ordem matemática do universo. Mas é o facto do material ser translúcido e permitir a filtragem da luz solar que lhe acrescenta encanto. Graças a esta singularidade torna-se mais do que uma metáfora da cúpula celeste porque nela se projecta o Sol, efectivamente. Um saboroso toque aristotélico no seio duma concepção neoplatónica do cosmos. |
||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
|
Igreja de Santa Maria da Graça
|
||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
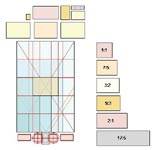
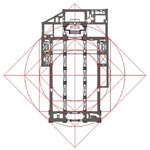
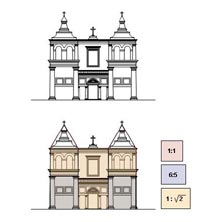
Santa Maria da Graça de Setúbal, tal como a São Pedro de Palmela, filia-se, tipologicamente, nas igrejas de três naves, um programa com tradição e que, pela sua comprovada adequação à prática de culto, resistirá ao tipo de igreja imposto pelo Concílio de Trento de que Il Gesù de Roma, de Vignola, se constituirá como principal modelo embora se conheçam, mesmo no nosso país, exemplares precedentes. Impõe-se este templo de Setúbal pelas suas generosas dimensões para uma igreja que não foi desde logo Sé. Impressiona, também, o desenho vigoroso da sua fachada principal com a presença dominante das torres, que avançam relativamente ao pano central, sem se salientar em altura. Flanqueiam uma galilé, com o tema recorrente da serliana (também patente na Capela das Onze Mil Virgens), onde se rasga o pórtico de entrada, de rigoroso traçado clássico, com réplicas, a menor escala, nas fachadas laterais. Essa antecâmara eleva-se a meia altura configurando uma varanda sobre a qual se abre um enorme janelão rectangular que inunda de luz o espaço de culto e dirige o Sol Poente para o Altar. A geometria do templo é também ad quadratum, mas não é evidente a sua detecção. Em planta o rectângulo que corresponde ao conjunto das 3 naves tem a particularidade de ao ser subdividido em 5 partes, quer no comprimento, quer na largura, dar origem a um rectângulo homotético do primeiro cujo comprimento determina o ritmo longitudinal dos tramos da colunata que, naturalmente, são 5. Por sua vez o afastamento das duas fiadas de colunas, que definem a largura da nave central, é estabelecido de modo a que cada tramo corresponda a um rectângulo 7:5, convergente com o rectângulo |
||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
|
A fachada é um rectângulo |
||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
|
Geometria e Arquitectura
Apesar de António Rodrigues considerar que para aquele que houver de fazer profissão de arquitecto é necessário que seya muzico para que hemtẽda as porposois das vozes, porque por estas porposoys ẽtemdera as proposois que am de ter seus edefisios 6 , parece-me que as relações proporcionais que utiliza não são explicáveis somente à luz da teoria musical. Têm um sentido matemático próprio, que se pode relacionar circunstancialmente com os intervalos musicais, mas decorre essencialmente da lógica intrínseca de cada edifício. Agora, o que é fundamental, como o próprio adverte, tal como Vitrúvio, é que he nesessario ser esperto na Giometria 7 . Porque essa sim será a maneira de lançar pontes entre o real e o transcendente. E que couza he giometria? questiona-se António Rodrigues…para logo esclarecer: Gyometria não he outra couza que feguras, as quais nam se podem fazer sem linhas, e amgulos, e pomto... Pola dita Geometria se vera como não se pode fazer nada sem hela, nem ha Arte matematica não se hemtemdera bem sem ser esperto na Giometria haquele que dela se deleitar. Termina com uma recomendação que consideramos que vale sempre a pena seguir: Quem for coriozo desta harte estude Hoclides, e nele achará bem couza em que se desemfade 8 . Manuscritos originais BN, Cód. 3675 – Tratado de Arquitectura Militar BPMP, Ms. 95 – Proposições Matemáticas Bibliografia COELHO, Maria da Conceição Pires – Dom Pedro de Mascarenhas e Capela das Onze Mil Virgens em Alcácer do Sal. Brotéria, Lisboa. 113, 1981, p. 274-295. HORTA CORREIA, José Eduardo – A arquitectura: maneirismo e ‘estilo chão’. In SERRÃO, Vítor – História da Arte em Portugal, O Maneirismo. Lisboa: Publicações Alfa, 1993, vol. 7, p. 93-135. MOREIRA, Rafael – Arquitectura: Renascimento e Classicismo. In PEREIRA, Paulo – História da Arte Portuguesa. Lisboa: Círculo de Leitores, 1995, vol. II, p. 303-375. MOREIRA, Rafael – Um tratado português de arquitectura do séc. XVI (1576-1579). Lisboa: FCSH-UNL, 1982. Tese de Mestrado em História da Arte. SEGURADO, Jorge – Francisco d’Ollanda. Lisboa: Edições Excelsior, 1961. SOROMENHO, Miguel – Classicismo, italianismo e ‘estilo chão’. O ciclo filipino. In PEREIRA, Paulo – História da Arte Portuguesa. Lisboa: Círculo de Leitores, 1995, vol. II, p. 377-403. VIEIRA DA SILVA, José Custódio – Setúbal. Lisboa: Editorial Presença, 1990. VITERBO, Sousa – Dicionário Histórico e Documental dos Arquitectos, Engenheiros e Construtores Portugueses. Lisboa: INCM, 1988, 2 vol. Reprodução em fac-símile do exemplar com data de 1899 da Biblioteca da INCM. XAVIER, João Pedro – António Rodrigues, a Portuguese Architect with a Scientific Inclination. NEXUS IV – Architecture and Mathematics. Ed. WILLIAMS, Kim; RODRIGUES, José Francisco. Fuccechio: Kim Williams Books, 2002, p. 253-268. Notas 1 Cf. MOREIRA, Rafael – Arquitectura: Renascimento e Classicismo. In PEREIRA, Paulo – História da Arte Portuguesa. Lisboa: Círculo de Leitores, 1995, vol. II, p. 355. 2 Ver MOREIRA, Rafael – Um tratado português de arquitectura do séc. XVI (1576-1579). Lisboa: FCSH-UNL, 1982. Tese de Mestrado em História da Arte. 3 Pela documentação da Chancelaria de D. Sebastião e D. Henrique sabe-se que possuiu cinco “moios” de trigo em terras de Alcácer. 4 Além destas obras é certo que a Igreja de São Pedro de Palmela, Igreja de Nossa Senhora da Consolação de Alcácer, profundamente adulterada, bem como a antiga Igreja da Anunciada de Setúbal, desaparecida com o terramoto, são de sua autoria, assim como a Sala do Capítulo e Sacristia (de que só resta um portal e duas janelas) do Convento de Jesus de Setúbal. 5 Proposição 2 das “Proposições Matemáticas” (BPMP, Ms. 95). 6 BN, Cod. 3675, fol. 10 v. 7 Idem 8 Ibidem fol. 25 v. Este texto constitui parte da introdução ao “Capitolo em que se declara que couza he Giometria” |
||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
| © Instituto Camões 2004 | ||||||||||||||||||||||||||||||||||||||||