In the mid-fifteenth century, pilots found a way to estimate the latitude of their location. They used a fact known since antiquity: the altitude of the celestial bodies depends on the latitude. From that moment on, measuring the altitude of the stars and the planets became vital for navigation and processes were sought to perfect the measuring method. Other instruments soon joined the quadrant, the astrolabe and the cross staff. Pedro Nunes invented the nonius, a process of subdividing the scales, and other instruments of innovative design.

In order to permit greater precision in measuring the altitude of the sun, Pedro Nunes invented an instrument that came to be known as the nautical ring, astronomical ring or graduated ring. His idea is described in one of his works published in 1573 in Coimbra, De arte atque ratione navigandi libri duo, where the mathematician refers to it merely as astrolabe, as its design is very similar to that of a nautical astrolabe from which the centre pin is removed

The instrument was simply made up of a ring with another smaller ring from which it could be hung vertically. A pinhole was situated 45º from the hanging point. The ring was held vertically in such a way that the rays of the sun shone through the pinhole onto the scale on the inside of the ring. The altitude of the sun was measured on this scale.

There are several old images of this instrument. The first one known to have some detail and which gives some indication of its construction and use is the one that Manuel Pimentel included in his work Arte de Navegar, published in Lisbon in 1712. The illustrations that appeared previously, both the original by Pedro Nunes of 1573 and the next reproduction that is known, of the Regimiento de Navigación by the Spanish André Garcia de Cespedes, published in Madrid in 1606, are very schematic.

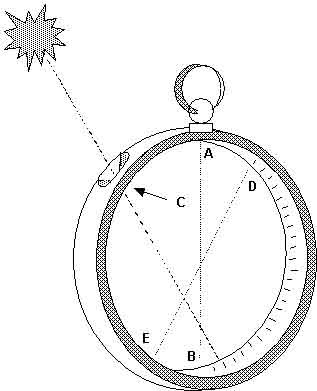
The nautical ring made it possible to read the altitude of the sun on a graduated scale marked on the inside of the ring, on the EBD arc. The rays of the sun shone through pinhole C and were projected onto this scale. With the ring hung from the smaller ring A, line AB remained vertical. In this way, if the sun was at its zenith, the light would e projected onto point E, marking an altitude of 90º. If it was on the horizon, its light would be projected onto point D, marking an altitude of 0º. It should be noted, therefore, that the point of projection travels 180º while the altitude of the sun varies only 90º. This is the great theoretical advantage of the instrument, as each degree in altitude corresponds to two degrees on the device, which should permit twofold accuracy. (drawing by prof. Susana Nápoles).

Pedro Nunes gives several practical indications for the construction of the instrument. He recommends that the ring have the thickness of “one finger” (a measurement used at the time and which is equivalent to little more than 2 cm) and insists that the pinhole should be as small as possible. He further explains that it was necessary “to cut a certain part in the form of an angle”, marked GCF on the picture, so that the rays of the sun could pass through the pinhole, irrespective of the position of the sun. “Because of the part of metal that was removed from the instrument,” he continues, “the ring becomes less heavy” on that side; in order to keep it exactly vertical, it would therefore be necessary to compensate for the loss in weight and “to remove the same quantity of metal from the other side”.

The advantage of the nautical ring over an astrolabe would normally be, according to Nunes, that the markings on the EBD scale “are twice as big on this instrument than they would be if an alidade revolved on its centrepiece, as can be seen in the traditional astrolabe”.

The nautical ring is based on a geometrical property which Euclides demonstrates in proposition 20 of book III of his Elements and which Nunes expressly refers to, reporting that the angle “which is on the circumference of the circle contains an arc double of the vertex in the centre”. Stated in modern language, the angle at the centre, i.e. with its vertex in the centre of the astrolabe, is double the inscribed angle, i.e. with its vertex in C.

The nautical ring is an ingenious application of geometry and was praised by some scholars of the time. It did, however, have one inconvenience that made the advantage imagined by Nunes an illusion: as tiny as the pinhole might be, the light projected by the sun onto the inside of the graduated arc could never be reduced to a point, given that our star does not appear to us as a point but rather as a disk. As this disk has a diameter of approximately half a degree, the image projected occupies at least half a degree, thereby reducing the precision of the instrument. This inconvenience would not exist if the intention were to measure the altitude of the stars; however, their brightness is not strong enough to be visibly projected through the graduated arc.

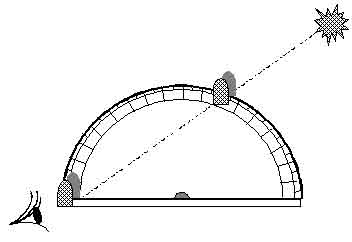
	Functioning scheme of the graduated semicircle. In this instrument, the altitude of the celestial body corresponds to the angle between the base and the orientation of the movable sighting device and is measured on the scale of the semicircle. If the sighting device is precisely constructed, advantage is taken of Pedro Nunes’ initial idea as each degree in altitude corresponds to two degrees of the angle at the centre. (Drawing by prof. Susana Nápoles)

Nunes’ invention appears to give us a glimpse of a characteristic common to many of his works. The cosmographer had a command of geometry and mathematics as well as an extraordinary creative spirit that lead him to conceive imaginative and potentially useful instruments. Nevertheless, his inexperience in the use of instruments resulted in many of his proposals not being as effective as he had imagined. Many of Pedro Nunes’ basic ideas, however, could and did have fruitful applications later on, as is the case of this instrument, which did not prove useful to navigation, but which gave rise to several others, among which the so-called graduated semicircle. This instrument had a movable sighting device, which could be pointed at a star and read its altitude on a scale similar to that of the nautical ring. The idea of duplicating the angle in the measuring scale proved to be a highly fruitful idea after all.


Nuno Crato