|
From the Kiblah of Al-Biruni to the Loxodrome of Pedro Nunes
 |
|
|
|
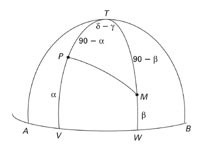
The kiblah problem: given the latitude and longitude coordinates of two points, find the direction PQ, which intersects the place where the believer finds himself, P, with Mecca, M, along a great circle arc over the terrestrial sphere.
|
|
|
|
In the Muslim civilisation, the oldest known study on Geometry is by the famous Muhammad ibn Musa al-Khwarizmi (c. 780–850), a mathematician of Persian origin who was among the first members of the “House of Wisdom” (Bait al-Hikma) in Baghdad. In al-Khwarizmi, geometry appears at the service of algebraic demonstrations, as it did for many ensuing centuries. Islamic geometricians, however, went way beyond that, being the direct precursors of Pedro Nunes in studying certain problems of spherical trigonometry, the branch of geometry that would later become a crucial instrument for navigation.
The Islamites studied the angles of triangles on the surface of the terrestrial sphere, spurred by a religious problem of interesting geometric implications: the kiblah problem, i.e. the direction of Mecca. As is common knowledge, Muslims must pray facing the holy city, which raises the problem of the precise determination of the direction of this city from any given point on the globe. The problem is easy to solve with reasonable accuracy in the vicinity of Mecca; however it became difficult when the Islamic civilisation spread to the Iberian Peninsula, to the African continent and to other places far away from Arabia. Al-Biruni created a precise method to determine the direction of Mecca given the coordinates of the place in which the believer finds himself. The problem was taken up again later by Pedro Nunes in navigation. The Portuguese mathematician was interested in determining the direction a ship should follow in order to reach its destination. His problem generalises the kiblah problem, turning it into a dynamic problem. The shortest route, a great circle route, is not generally given by a steady compass course, and requires constant adjustment throughout the journey in order to keep the ship on this optimal route. The shortest route became known as orthodrome, or great circle route, and is not the constant cardinal direction, later known as loxodrome, or rhumb line. The difference between the two routes was one of the greatest feats of Pedro Nunes.
The problems of spherical trigonometry are of great interest to nautical theory. However, the Arabs left the Western world, namely the Iberians, with a wealth of navigational knowledge and techniques which became crucial for the Discoveries. These include the lateen sail (triangular sail), astronomical expertise for determining coordinates, namely sun height tables, nautical charts and other geographical knowledge. Even after the Portuguese successfully rounded the coasts of Africa, the help from an Arab pilot to navigate the Indian Ocean proved invaluable. As Camões states (Lusíadas, VI, 5):
- In his new pilot there was no deceit,
Just an expert knowledge of the course,
So he cruised now with greater ease of mind
Than in the latitudes they left behind.
Nuno Crato
|
|