|
Sobre os conteúdos
Os conteúdos trabalhados e disponibilizados no âmbito do projecto Temanet consistem num conjunto de wordnets parciais do Português, delimitadas de acordo com doze domínios semânticos: Alimentação, Arte, Comunicação, Desporto, Educação, Geografia, Habitação, Relações Humanas, Saúde, Seres Vivos, Transportes e Vestuário.
Uma wordnet é uma rede léxico-conceptual que inclui expressões lexicais que representam conceitos, ligadas entre si por relações de diversos tipos. Das relações estruturantes, destacam-se as relações de sinonímia, hiponímia/hiperoníma e meronímia/holonímia. Adicionalmente é também especificado um grande número de relações que envolvem a estrutura dos eventos e as entidades neles participantes, genericamente designadas como relações de função, bem como relações que permitem definir o significado de cada nó da rede com maior precisão, em particular uma séria de relações inter-categoriais. [para saber mais]
A cada expressão é ainda associada uma definição informal de cada conceito e um exemplo que evidencia restrições sintácticas e semânticas dos itens lexicais em causa. Para além de ilustrar o comportamento sintáctico-semântico dos membros do conjunto de sinónimos considerado, os exemplos veiculam também conhecimento enciclopédico, quando pertinente. São ainda assinalados registos marcados, em particular relativos a origem e contexto pragmático, por exemplo.
Toda esta informação codificada é tornada acessível ao utilizador através de uma interface flexível e intuitiva, que permite uma navegação ágil intra- e inter-redes.
A apresentação da informação em cada entrada
Ao seleccionar uma determinada expressão para consulta, seja através da pesquisa livre, seja através das listas organizadas alfabeticamente para cada domínio, tem acesso a toda a informação referida na secção anterior, apresentada tal como ilustrado abaixo.
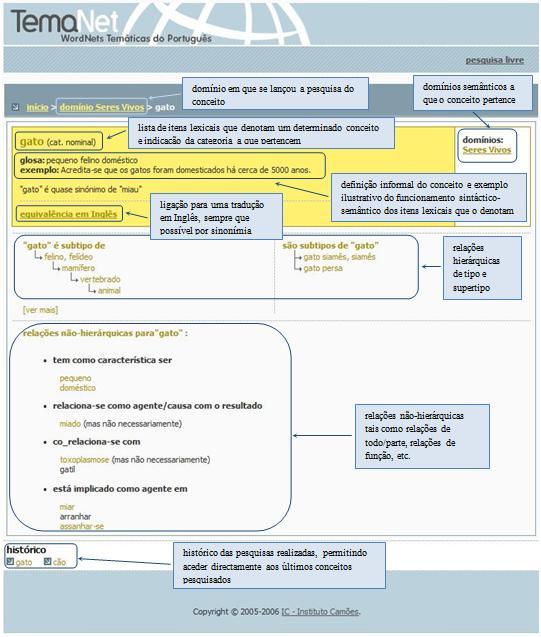
Adicionalmente, e quando a expressão seleccionada faça parte de uma subrede com grande profundidade, poderá visualizar mais níveis, tanto de subtipos como de supertipos (sempre que estes estejam disponíveis para o conceito consultado), clicando na expressão [ver mais], tal como apresentado abaixo.
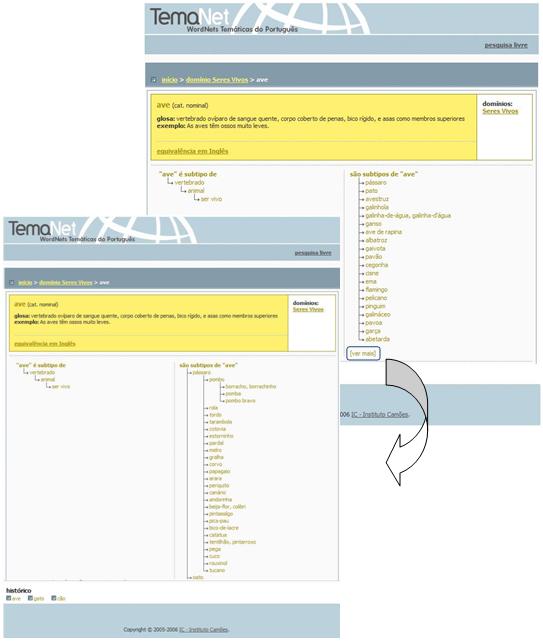
Outro aspecto a sublinhar no que respeita à navegação na interface prende-se com a possibilidade de passar de um conceito a outro com ele relacionado clicando apenas na expressão que o denota, dado que todos os conceitos referidos numa entrada que está a ser consultada, desde que estejam codificados na base de dados do Temanet, são ligações para a entrada em que são caracterizados, independentemente de esta pertencer ao mesmo domínio semântico ou a outro. Note-se que a passagem de um domínio semântico a outro torna-se evidente para o utilizador através da associação de cada domínio a uma cor diferente, tal como ilustrado na imagem abaixo.
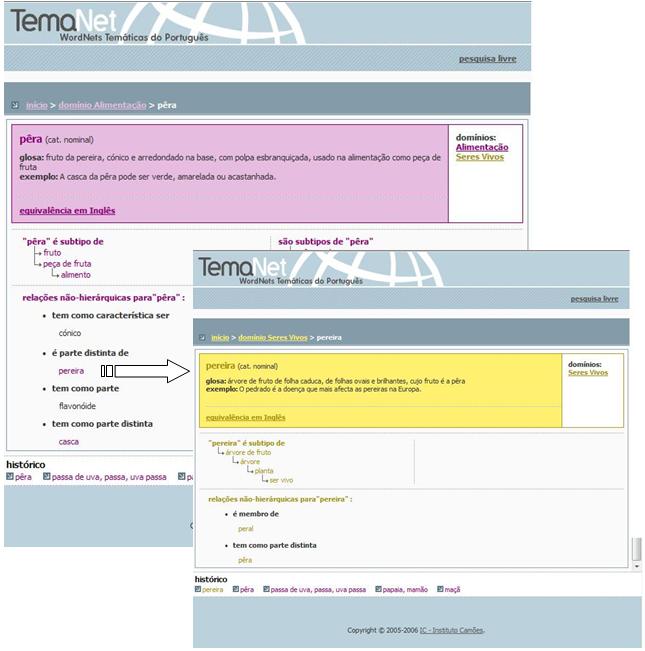
As relações léxico-conceptuais expressas na rede
Tal como referido na primeira secção desta página, existe uma grande diversidade de relações léxico-conceptuais expressas nas wordnets que integram a base de dados do projecto Temanet e que podem ser consultadas nas páginas de resultados apresentadas para cada conceito pesquisado. Nesta secção explicita-se, com a ajuda de exemplos, em que consiste cada uma das relações utilizadas na organização da rede de conceitos disponibilizados.
As relações implementadas neste projecto são as seguintes:
[topo]
relações geral/específico
 x é supertipo de
A relação de supertipo (hiperonímia) é uma relação assimétrica, inversa da relação de subtipo, que corresponde grosso modo à noção de definição de uma classe. Em termos informais, os supertipos devem respeitar as seguintes condições:
A é supertipo de B
se
A não é um (tipo de) B
e
B é um (tipo de) A
Vejamos os seguintes exemplos:
a. Se o João comprou um veículo então o João comprou um automóvel. Falso
b. Se o João comprou um automóvel então o João comprou um veículo. Verdadeiro
c. Se A é um veículo, A não é um (tipo de) automóvel
d. Se B é um automóvel, B é um (tipo de) veículo
Logo: veículo é supertipo de automóvel (e automóvel é subtipo de veículo)
Estes exemplos evidenciam uma maior especificidade de automóvel relativamente a veículo, ou seja, automóvel tem todas as propriedades de veículo (e mais algumas), mas veículo não tem todas as propriedades de automóvel. Esta relação implica que o supertipo pode substituir os seus subtipos em contextos referenciais, mas que o inverso não se verifica. Este facto é particularmente evidente em contextos de recuperação anafórica, em que o supertipo retoma o conteúdo de um seu subtipo.
e.O João trouxe o automóvel do irmão. Este veículo é de cor cinzenta.
[voltar à tabela]
x é subtipo de
A relação de subtipo (hiponímia) é uma relação assimétrica, inversa da relação de supertipo, e que corresponde grosso modo à noção de pertença a uma classe. Em termos informais, os subtipos devem respeitar as seguintes condições:
A é subtipo de B
se
A é um (tipo de) B
e
B não é um (tipo de) A
Vejamos os seguintes exemplos:
a. Se o João bebeu uma bica então o João bebeu um café. Verdadeiro
b. Se o João bebeu um café então o João bebeu uma bica. Falso
c. Se A é uma bica , A é um (tipo de) café
d. Se B é um café, B não é um (tipo de) bica
Logo: bica é subtipo de café (e café é supertipo de bica)
Estes exemplos evidenciam uma maior especificidade de bica relativamente a café, ou seja, bica tem todas as propriedades de café (e mais algumas), mas café não tem todas as propriedades de bica.
[voltar à tabela]
x é instanciado por
Pode dizer-se dos nomes comuns, que designam classes de entidades, que são exemplificados por uma dada entidade individual (designada por um nome próprio). Para exprimir esta relação assimétrica entre uma classe de entidades e a entidade individual que a instancia utiliza-se a relação de instanciação. Em termos informais, para que A seja instanciado por B devem respeitar-se as seguintes condições:
A é instanciado por B
se
B é um nome próprio,
B é um A
e
A não é um B
Vejamos os seguintes exemplos:
a. Se a Ana visitou Praga então a Ana visitou uma cidade. Verdadeiro
b. Se a Ana visitou uma cidade então a Ana visitou Praga. Falso
Logo: cidade é instanciada por Praga
[voltar à tabela]
x é instanciação de
Pode dizer-se das entidades individuais, designadas pelos nomes próprios, que são exemplo de uma determinada classe de entidades (designada por um nome comum). Para exprimir esta relação assimétrica entre uma entidade individual e a classe que instancia utiliza-se a relação de instanciação. Em termos informais, para que A seja uma instanciação de B devem respeitar-se as seguintes condições:
A é instanciação de B
se
A é um nome próprio,
A é um B
e
B não é um A
Vejamos os seguintes exemplos:
a. Se a Ana trabalha na Serra da Estrela então a Ana trabalha numa montanha. Verdadeiro
b. Se a Ana trabalha numa montanha então a Ana trabalha na Serra da Estrela. Falso
Logo: Serra da Estrela é instanciação de montanha
[voltar à tabela]
relações todo/parte
Mais do que uma relação, a ligação entre o todo e as partes corresponde a uma complexa família de relações cuja não uniformidade diz respeito a aspectos como o grau de integração, de independência e de motivação da parte relativamente ao todo. Trata-se de uma relação assimétrica que pode ainda ser facultativa em qualquer dos dois sentidos, como no caso de puxador e porta, em que puxador é parte de porta, mas não necessariamente, podendo ser também parte de gaveta, janela ou portão, por exemplo, e porta tem como parte puxador, mas não necessariamente. Assim, para além de assimétrica, esta é também uma relação com restrições.
x tem como parte
Em termos informais, e de um modo geral, podemos definir esta família de relações nos seguintes termos:
A tem como parte B
se
B faz parte de A
e A tem B
Neste caso, por exemplo, corpo tem uma cabeça e cabeça faz parte de corpo, não sendo o inverso verdade: cabeça não tem um corpo e corpo não faz parte de cabeça. Logo corpo tem como parte cabeça.
[voltar à tabela]
x é parte de
Em termos informais, e de um modo geral, podemos definir esta família de relações nos seguintes termos:
A é parte de B
se
A faz parte de B
e B tem A
Neste caso, por exemplo, cabeça faz parte de corpo e corpo tem uma cabeça, não sendo o inverso verdade: corpo não faz parte de cabeça e cabeça não tem um corpo. Logo cabeça é parte de corpo.
[voltar à tabela]
x tem como membro
Um dos subtipos de relação entre o todo e a parte é aquele que se estabelece entre um conjunto de entidades e os seus membros. Esta relação pode definir-se informalmente nos seguintes termos:
A tem como membro B
se
A é um conjunto de entidades
B é um objecto singular
e
B é um elemento de A
e A é um conjunto que inclui B
Neste caso, por exemplo, alcateia é um conjunto que inclui lobos e lobo é um elemento de alcateia, não sendo o inverso verdade: lobo não é um conjunto que inclui alcateias e alcateia não é um elemento de lobo. Logo alcateia tem como membro lobo.
[voltar à tabela]
x é membro de
Um dos subtipos de relação entre o todo e a parte é aquele que se estabelece entre um conjunto de entidades e os seus membros. Esta relação pode definir-se informalmente nos seguintes termos:
A é membro de B
se
B é um conjunto de entidades
A é um objecto singular
e
A é um elemento de B
e B é um conjunto que inclui A
Neste caso, por exemplo, lobo é um elemento de alcateia e alcateia é um conjunto de lobos, não sendo o inverso verdade: alcateia não é um elemento de lobo e lobo não é um conjunto de alcateias. Logo lobo é membro de alcateia.
[voltar à tabela]
x tem como parte distinta
Um dos subtipos de relação entre o todo e a parte é aquele que se estabelece entre um nome considerado como um todo e as suas partes constituintes. Esta relação pode definir-se informalmente nos seguintes termos:
A tem como parte distinta B
se
A é constituído por diversas partes constituintes
e
B é uma componente distinta de A
e A é um todo em cujas componentes se inclui B
Neste caso, por exemplo, aparelho respiratório é um todo em cujas componentes se inclui nariz e nariz é uma componente de aparelho respiratório, não sendo o inverso verdade: nariz não é um todo em cujas componentes se inclui aparelho respiratório e aparelho respiratório não é uma componente de nariz. Logo aparelho respiratório tem como parte distinta nariz.
[voltar à tabela]
x é parte distinta de
Um dos subtipos de relação entre o todo e a parte é aquele que se estabelece entre um nome considerado como um todo e as suas partes constituintes. Esta relação pode definir-se informalmente nos seguintes termos:
A é parte distinta de B
se
B é constituído por diversas partes constituintes
e
A é uma componente distinta de B
e B é um todo em cujas componentes se inclui A
Neste caso, por exemplo, nariz é uma componente distinta de aparelho respiratório e aparelho respiratório é um todo em cujas componentes se inclui nariz, não sendo o inverso verdade: aparelho respiratório não é uma componente distinta de nariz e nariz não é um todo em cujas componentes se inclui aparelho respiratório. Logo nariz é parte distinta de aparelho respiratório.
[voltar à tabela]
x tem como porção
Um dos subtipos de relação entre o todo e a parte é aquele que se estabelece entre uma porção e o todo do qual esta foi separada. Esta é uma relação todo/parte atípica porque o todo é sempre pré-existente em relação à porção e as fronteiras da porção não são definidas, pelo que, regra geral, esta não é lexicalizada. Informalmente podemos definir esta relação nos seguintes termos:
A tem como porção B
se
A e B são substâncias
B é uma quantidade
e
B é uma porção de A
e A não é uma porção de B
Neste caso, por exemplo, gota é uma porção de líquido e líquido não é uma porção de gota. Logo líquido tem como porção gota.
[voltar à tabela]
x é porção de
Um dos subtipos de relação entre o todo e a parte é aquele que se estabelece entre uma porção e o todo do qual esta foi separada. Esta é uma relação todo/parte atípica porque o todo é sempre pré-existente em relação à porção e as fronteiras da porção não são definidas, pelo que, regra geral, esta não é lexicalizada. Informalmente podemos definir esta relação nos seguintes termos:
A é porção de B
se
A e B são substâncias
A é uma quantidade
e
A é uma porção de B
e B não é uma porção de A
Neste caso, por exemplo, gota é uma porção de líquido e líquido não é uma porção de gota. Logo gota é porção de líquido.
[voltar à tabela]
x tem como substância/material
Um dos subtipos de relação entre o todo e a parte é aquele que se estabelece entre uma entidade concreta e a substância de que esta é feita. Esta relação pode definir-se informalmente nos seguintes termos:
A tem como substância/material B
se
A é uma entidade concreta
B é uma substância
e
A é feito de B
e B não é feito de A
Neste caso, por exemplo, enchido é feito de carne de porco e carne de porco não é feito de enchido. Logo enchido tem como substância/material carne de porco.
[voltar à tabela]
x é substância/material de
Um dos subtipos de relação entre o todo e a parte é aquele que se estabelece entre uma entidade concreta e a substância de que esta é feita. Esta relação pode definir-se informalmente nos seguintes termos:
A é substância/material de B
se
A é uma entidade concreta
B é uma substância
e
B é feito de A
e A não é feito de B
Neste caso, por exemplo, enchido é feito de carne de porco e carne de porco não é feito de enchido. Logo carne de porco é substância/material de enchido (mas não necessariamente).
[voltar à tabela]
x tem como localização
Um dos subtipos de relação entre o todo e a parte é aquele que se estabelece entre uma zona e uma zona mais vasta que inclui a primeira. Esta relação pode definir-se informalmente nos seguintes termos:
A tem como localização B
se
A e B são entidades concretas
A é uma zona mais vasta que B
e
B é uma zona localizada em A
e A não é uma zona localizada em B
Neste caso, por exemplo, cidade é uma zona mais vasta que baixa, baixa é uma zona localizada numa cidade e cidade não é uma zona localizada numa baixa. Logo cidade tem como localização baixa.
[voltar à tabela]
x é localização de
Um dos subtipos de relação entre o todo e a parte é aquele que se estabelece entre uma zona e uma zona mais vasta que inclui a primeira. Esta relação pode definir-se informalmente nos seguintes termos:
A é localização de B
se
A e B são entidades concretas
B é uma zona mais vasta que A
e
A é uma zona localizada em B
e B não é uma zona localizada em A
Neste caso, por exemplo, cidade é uma zona mais vasta que baixa, baixa é uma zona localizada numa cidade e cidade não é uma zona localizada numa baixa. Logo baixa é localização de cidade.
[voltar à tabela]
relações de equivalência
x é sinónimo de
A relação de sinonímia é uma relação básica na construção de uma wordnet. Cada nó da rede representa um conceito e especifica todas as lexicalizações desse conceito (um conjunto de sinónimos).
No sentido original, a relação de sinonímia entre duas expressões é entendida como uma relação absoluta, definida relativamente ao impacto que a substituição de uma pela outra tem numa frase em termos de valor de verdade. Em termos informais, os sinónimos absolutos ou verdadeiros, devem respeitar as seguintes condições:
A e B são sinónimos se e só se a substituição de A por B ou de B por A nunca alterar o valor de verdade da frase em que a substituição se verifica.
Por razões de economia, a sinonímia absoluta é um fenómeno raro, razão pela qual no quadro das wordnets a sinonímia deve entender-se num sentido mais fraco, com referência a um contexto. Este conceito é definido em Miller e Fellbaum (1990) nos seguintes termos:
“duas expressões são sinónimas num contexto linguístico C se a substituição de uma por outra em C não altera o valor de verdade de C”
Assim, na decisão quanto à existência de uma relação de sinonímia entre unidades lexicais, apoiada em testes linguísticos, uma das variáveis a ser tida em conta é o domínio semântico. Outro aspecto crucial a considerar é a simetria da relação de sinonímia que podemos observar abaixo.
se A e B são sinónimos (em C)
então
(i) um A é um B
e
(ii) um B é um A
Esta simetria, e este teste em particular, permite identificar as verdadeiras relações de sinonímia, distinguindo-as de pares de unidades lexicais que satisfazem o teste da substituição.
a. O João estacionou o automóvel num local escuro.
b. O João estacionou a viatura num local escuro.
c. Se A é um automóvel então A é uma viatura. Verdadeiro
d. Se B é uma viatura então B é um automóvel. Falso
Logo: A é um B não implica B é um A. => A e B não são sinónimos
e. O João partiu o dedo mínimo.
f. O João partiu o dedo mindinho.
g. Se A é um dedo mínimo então A é um dedo mindinho. Verdadeiro
h. Se B é um dedo mindinho então B é um dedo mínimo. Verdadeiro
Logo: A é um B implica B é um A. => A e B são sinónimos
[voltar à tabela]
x é quase sinónimo de
Em alguns casos, existem palavras que estabelecem entre si relações de grande proximidade sem que possamos, no entanto, considerá-las sinónimas, nomeadamente por não se comportarem em relação aos testes de substituição e de simetria tal como estabelecido na definição de sinonímia.
Para exprimir esta relação de quase-equivalência entre dois conceitos existe a relação de quase sinonímia. A quase sinonímia é também ela uma relação simétrica e é definida pelas seguintes condições:
se A e B são quase sinónimos
então
(i) um A é uma espécie de B
e
(ii) um B é uma espécie de A
Desta forma, a quase sinonímia permite-nos exprimir a existência de uma relação privilegiada de proximidade semântica entre co-hipónimos (conceitos que partilham um mesmo supertipo) que não chega, no entanto, a ser uma relação de equivalência.
a. Se A é um ananás então A é uma espécie de abacaxi Verdadeiro
b. Se B é um abacaxi então B é uma espécie de ananás Verdadeiro
Logo: ananás e abacaxi são quase sinónimos
[voltar à tabela]
x é sinónimo transcategorial de
Embora existam por vezes pequenas nuances de significado - a redução de argumentos das nominalizações, por exemplo - há nas línguas a possibilidade de denotar a mesma situação ou evento usando unidades lexicais de diferentes categorias gramaticais. Entre estas diferentes unidades lexicais existe portanto uma relação de correspondência transcategorial que, tal como as outras relações de equivalência, é uma relação simétrica que obedece às seguintes condições:
se A e B têm correspondência transcategorial
então
(i) se há uma situação de A, então alguma coisa B
e
(ii) se alguma coisa B, então há uma situação de A
Vejamos um exemplo para tornar esta definição mais clara:
a. Se há uma situação de movimento, então há alguma coisa que se move Verdadeiro
b. Se alguma coisa se move, então há uma situação de movimento Verdadeiro
Logo: movimento e mover são sinónimos transcategoriais
[voltar à tabela]
relações de oposição
x é antónimo de
A relação de antonímia é uma relação simétrica que exprime oposição conceptual entre dois nós na rede. Os antónimos constituem categorias contrastantes numa mesma dimensão, ou seja, entre as condições para que se verifique a relação de antonímia entre dois itens encontra-se, não só o contraste, mas também algumas propriedades partilhadas. Estas propriedades partilhadas correspondem, por exemplo, à existência de uma relação de co-hiponímia entre antónimos, em particular no caso de nomes e verbos antónimos. Assim, em termos informais, podemos definir as condições a que obedece a relação de antonímia do seguinte modo:
A e B são antónimos
se
A e B são ambos um tipo de C
e
(i) se X é A
então
(ii) X não é B
e
(iii) se X é B então não é A
Vejamos um exemplo para tornar esta definição mais clara:
a. Se entrar e sair são ambos mover-se
b. Se uma entidade sai, então essa mesma entidade não entra
c. Se uma entidade entra, então essa mesma entidade não sai
Logo: entrar é antónimo de sair e sair é antónimo de entrar
Um outro aspecto crucial no que respeita a esta relação é o seu estatuto: a antonímia é determinada ao nível lexical, não basta que se verifique oposição conceptual para que duas palavras sejam antónimas. Assim, por exemplo, embora comprido e longo sejam sinónimos e se oponham conceptualmente a curto, apenas curto e comprido são antónimos. Deste modo esta é uma relação entre itens lexicais e não entre conjuntos de sinónimos (i.e. nós da rede).
[voltar à tabela]
x é quase antónimo de
A relação de quase antonímia é uma relação simétrica que exprime oposição conceptual entre dois nós na rede. Os quase antónimos constituem categorias contrastantes numa mesma dimensão, ou seja, tal como vimos para a relação de antonímia, entre dois itens quase antónimos verifica-se, não só um contraste, mas também algumas propriedades partilhadas. Estas propriedades partilhadas correspondem, por exemplo, à existência de uma relação de co-hiponímia entre quase antónimos, em particular no caso de nomes e verbos quase antónimos.
Ao contrário do que acontece com a relação de antonímia, a relação de quase antonímia corresponde apenas a oposição conceptual entre dois nós na rede e é, por isso, uma relação entre conjuntos de sinónimos.
Em termos informais, podemos definir as condições a que obedece a relação de quase antonímia do seguinte modo:
A e B são quase antónimos
se
A e B são ambos um tipo de C
e
(i) se X é A
então
(ii) X não é B
e
(iii) se X é B então não é A
Vejamos um exemplo para tornar esta definição mais clara:
a. Se negro e branco são ambos cores
b. Se existe uma entidade que é negra, então essa mesma entidade não é banca
c. Se existe uma entidade que é branca, então essa mesma entidade não é negra
Logo: negro é quase antónimo de branco e branco é quase antónimo de negro
[voltar à tabela]
relações de categorização
x é caracterizável por
Uma das características mais prototípicas dos adjectivos consiste no papel que desempenham relativamente ao nome. Para a grande classe dos adjectivos descritivos este papel consiste em atribuir um valor de um atributo ao nome modificado. Existe, assim, uma relação privilegiada entre cada um destes adjectivos e um dado atributo. A relação é caracterizável por explicita esta ligação. Trata-se de uma relação assimétrica que pode definir-se informalmente nos seguintes termos:
A é caracterizável por B
se
A é um nome denotador de uma propriedade
B é um adjectivo
e
B fixa um valor do atributo A
Por exemplo, alto fixa um valor do atributo altura, determinando um valor elevado deste atributo. Logo altura é caracterizável por alto. Esta relação é inversa da relação caracteriza quanto a pelo que se altura é caracterizável por alto, então alto caracteriza quanto a altura.
[voltar à tabela]
x caracteriza quanto a
A relação caracteriza quanto a explicita a ligação entre um adjectivo e um dado atributo. Trata-se de uma relação assimétrica que pode definir-se informalmente nos seguintes termos:
A caracteriza quanto a B
se
A é um adjectivo
B é um nome denotador de uma propriedade
e
A fixa um valor do atributo B
Por exemplo, alto fixa um valor do atributo altura, determinando um valor elevado deste atributo. Logo alto caracteriza quanto a altura. Esta relação é inversa da relação é caracterizável por pelo que se alto caracteriza quanto a altura, então altura é caracterizável por alto.
[voltar à tabela]
x é característica de
Os nomes que partilham um mesmo supertipo (co-hipónimos) distinguem-se do seu supertipo e dos seus nós irmãos por uma determinada diferença específica. Estas propriedades distintivas dos nomes são frequentemente lexicalizadas por expressões adjectivais. A relação é característica de permite explicitar diferenças específicas na rede, ligando cada nome às expressões adjectivais que lexicalizam as suas propriedades distintivas. Trata-se de uma relação assimétrica, facultativa em ambos os sentidos, que pode definir-se informalmente nos seguintes termos:
A é característica de B
se
A é um adjectivo
B é um nome
e
A é uma propriedade distintiva de B
Por exemplo, carnívoro é uma propriedade distintiva de tubarão. Logo carnívoro é característica de tubarão. Esta relação é inversa da relação tem como característica ser pelo que se carnívoro é característica de tubarão, então tubarão tem como característica ser carnívoro.
[voltar à tabela]
x tem como característica ser
A relação tem como característica ser permite explicitar diferenças específicas na rede, ligando cada nome às expressões adjectivais que lexicalizam as suas propriedades distintivas. Trata-se de uma relação assimétrica, facultativa em ambos os sentidos, que pode definir-se informalmente nos seguintes termos:
A tem como característica ser B
se
A é um nome
B é um adjectivo
e
B é uma propriedade distintiva de A
Por exemplo, carnívoro é uma propriedade distintiva de tubarão. Logo tubarão tem como característica ser carnívoro. Esta relação é inversa da relação é característica de pelo que se tubarão tem como característica ser carnívoro, então carnívoro é característica de tubarão.
[voltar à tabela]
x está relacionado com
Uma das características mais prototípicas dos adjectivos consiste no papel que desempenham relativamente ao nome. Alguns adjectivos atribuem conjuntos de propriedades ao nome modificado, conjuntos de propriedades estes que geralmente correspondem à denotação de um outro nome. Existe, assim, uma relação privilegiada entre estes adjectivos e os nomes que lexicalizam os conjuntos de propriedades por eles atribuídos. A relação está relacionado com explicita esta ligação. Trata-se de uma relação subespecificada que pode definir-se informalmente nos seguintes termos:
A está relacionado com B (e B está relacionado com A)
se
A é um adjectivo
B é um nome
e
A atribui o conjunto de propriedades denotado por B
Por exemplo, aquático atribui o conjunto de propriedades denotado por água. Logo aquático está relacionado com água (e água está relacionado com aquático).
[voltar à tabela]
relações entre participantes num evento
x co_relaciona-se com
A noção de participação num determinado evento está incorporada no significado de alguns nomes, sem que esse evento seja necessariamente explicitado. As relações entre participantes num evento permitem correlacionar dois participantes num mesmo evento ou situação, com funções distintas.
A relação co_relaciona-se com é uma relação simétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite a explicitação desta correlação quando a função dos dois participantes é de alguma forma subespecificada, ou mais exactamente, quando não corresponde a nenhuma das funções temáticas tradicionalmente descritas na gramática. Assim, por exemplo, utiliza-se esta relação para exprimir a relação entre o conteúdo e o seu continente, como é o caso de bule e chá: bule é um recipiente próprio para servir chá e o chá é geralmente servido num bule, logo bule co_relaciona-se com chá e chá co_relaciona-se com bule.
[voltar à tabela]
x usa como instrumento
A relação usa como instrumento é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite a explicitação da correlação entre dois participantes cuja função é respectivamente a de agente e a de instrumento. Assim, usando esta relação podemos ligar nomes como pincel e pintor: um pintor é um artista que usa um pincel e o pincel é um instrumento usado geralmente por um pintor, logo pintor usa como instrumento pincel. Esta relação é inversa da relação é usado como instrumento por pelo que se pintor usa como instrumento pincel, então pincel é usado como instrumento por pintor (mas não necessariamente).
[voltar à tabela]
x é usado como instrumento por
A relação é usado como instrumento por é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite a explicitação da correlação entre dois participantes cuja função é respectivamente a de instrumento e a de agente sobre esse instrumento. Assim, usando esta relação podemos ligar nomes como pincel e pintor: o pincel é um instrumento usado geralmente por um pintor e pintor é um artista que usa um pincel, logo pincel é usado como instrumento por pintor (mas não necessariamente). Esta relação é inversa da relação usa como instrumento pelo que se pincel é usado como instrumento por pintor (mas não necessariamente), então pintor usa como instrumento pincel.
[voltar à tabela]
x relaciona-se como agente/causa com o resultado
A relação relaciona-se como agente/causa com o resultado é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite a explicitação da correlação entre dois participantes cuja função é respectivamente a de agente/causa e a de resultado. Assim, usando esta relação podemos ligar nomes como compositor e música: um compositor é um autor que cria músicas e uma música é uma obra artística criada por um compositor, logo compositor relaciona-se como agente/causa com o resultado música. Esta relação é inversa da relação relaciona-se como resultado com o agente/causa pelo que se compositor relaciona-se como agente/causa com o resultado música, então música relaciona-se como resultado com o agente/causa compositor.
[voltar à tabela]
x relaciona-se como resultado com o agente/causa
A relação relaciona-se como resultado com o agente/causa é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite a explicitação da correlação entre dois participantes cuja função é respectivamente a de resultado e a de agente/causa. Assim, usando esta relação podemos ligar nomes como música e compositor: uma música é uma obra artística criada por um compositor e um compositor é um autor que cria músicas, logo música relaciona-se como resultado com o agente/causa compositor. Esta relação é inversa da relação relaciona-se como agente/causa com o resultado pelo que se música relaciona-se como resultado com o agente/causa compositor, então compositor relaciona-se como agente/causa com o resultado música.
[voltar à tabela]
x é usado como instrumento para a obtenção de
A relação é usado como instrumento para a obtenção de é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite a explicitação da correlação entre dois participantes cuja função é respectivamente a de instrumento usado para se obter um dado resultado e a de resultado da acção desse instrumento. Assim, usando esta relação podemos ligar nomes como batedeira e claras em castelo: uma batedeira é um pequeno electrodoméstico que serve para obter claras em castelo e as claras em castelo são um preparado obtido pela acção de uma batedeira, logo batedeira é usado como instrumento para a obtenção de claras em castelo. Esta relação é inversa da relação obtém-se através da utilização de pelo que se batedeira é usado como instrumento para a obtenção de claras em castelo, então claras em castelo obtém-se através da utilização de batedeira (mas não necessariamente).
[voltar à tabela]
x obtém-se através da utilização de
A relação obtém-se através da utilização de é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite a explicitação da correlação entre dois participantes cuja função é respectivamente a de instrumento usado para se obter um dado resultado e a de resultado da acção desse instrumento. Assim, usando esta relação podemos ligar nomes como claras em castelo e batedeira: claras em castelo são um preparado geralmente obtido pela acção de uma batedeira e uma batedeira é um pequeno electrodoméstico que serve para obter claras em castelo, logo claras em castelo obtém-se através da utilização de batedeira (mas não necessariamente). Esta relação é inversa da relação é usado como instrumento para a obtenção de pelo que se claras em castelo obtém-se através da utilização de batedeira (mas não necessariamente), então batedeira é usado como instrumento para a obtenção de claras em castelo.
[voltar à tabela]
x relaciona-se como agente com o objecto
A relação relaciona-se como agente com o objecto é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite a explicitação da correlação entre dois participantes cuja função é respectivamente a de agente sobre um dado objecto e a de paciente, de objecto que sofre a acção desse agente. Assim, usando esta relação podemos ligar nomes como predador e presa: predador é um animal que caça presas e uma presa é um animal que é caçado por um predador, logo predador relaciona-se como agente com o objecto presa. Esta relação é inversa da relação relaciona-se como objecto com o agente pelo que se predador relaciona-se como agente com o objecto presa, então presa relaciona-se como objecto com o agente predador.
[voltar à tabela]
x relaciona-se como objecto com o agente
A relação relaciona-se como objecto com o agente é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite a explicitação da correlação entre dois participantes cuja função é respectivamente a de paciente, de objecto que sofre a acção de um dado agente e a de agente sobre esse mesmo objecto. Assim, usando esta relação podemos ligar nomes como presa e predador: uma presa é um animal que é caçado por um predador e predador é um animal que caça presas, logo presa relaciona-se como objecto com o agente predador. Esta relação é inversa da relação relaciona-se como agente com o objecto pelo que se presa relaciona-se como objecto com o agente predador, então predador relaciona-se como agente com o objecto presa.
[voltar à tabela]
x transforma-se em
A relação transforma-se em é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite a explicitação da correlação entre dois participantes cuja função é respectivamente a de paciente, de objecto que sofre uma dada acção, produzindo-se um dado resultado e a de resultado. Assim, usando esta relação podemos ligar nomes como clara e claras em castelo: clara é uma substância que é parte do ovo e que pode ser batida até se obterem claras em castelo e claras em castelo são um preparado obtido pela acção de bater claras, logo clara transforma-se em claras em castelo (mas não necessariamente). Esta relação é inversa da relação resulta da transformação de pelo que se clara transforma-se em claras em castelo (mas não necessariamente), então claras em castelo resulta da transformação de clara.
[voltar à tabela]
x resulta da transformação de
A relação resulta da transformação de é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite a explicitação da correlação entre dois participantes cuja função é respectivamente a de resultado e a de paciente, de objecto que sofre uma dada acção, produzindo-se um dado resultado. Assim, usando esta relação podemos ligar nomes como claras em castelo e clara: claras em castelo são um preparado obtido pela acção de bater claras e clara é uma substância que é parte do ovo e que pode ser batida até se obterem claras em castelo, logo claras em castelo resulta da transformação de clara. Esta relação é inversa da relação transforma-se em pelo que se claras em castelo resulta da transformação de clara, então clara transforma-se em claras em castelo (mas não necessariamente).
[voltar à tabela]
relações definidoras da estrutura do evento
x está envolvido em
A noção de função é um dos principais aspectos organizadores do conhecimento humano, reflectindo-se também de um modo muito particular no léxico. As línguas são ricas em processos derivacionais que geram novas palavras de acordo com uma dimensão funcional, criando por exemplo nomes a partir de verbos e vice-versa. As relações de envolvimento semântico vão permitir exprimir este tipo de correlações entre um dado evento e os participantes nesse mesmo evento.
A relação está envolvido em é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um participante cuja função é de alguma forma subespecificada, não correspondendo a nenhuma das funções temáticas tradicionalmente descritas na gramática, e o evento em que este participa. Esta relação pode definir-se informalmente nos seguintes termos:
A está envolvido em B
se
A é uma entidade
B é um evento ou situação
e
A está tipicamente envolvido na realização de B
Neste caso, por exemplo, agrafo está tipicamente envolvido na realização de agrafar. Logo agrafo está envolvido em agrafar. Esta relação é inversa da relação envolve pelo que se agrafo está envolvido em agrafar, então agrafar envolve agrafo.
[voltar à tabela]
x envolve
A relação envolve é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um participante cuja função é de alguma forma subespecificada, não correspondendo a nenhuma das funções temáticas tradicionalmente descritas na gramática, e o evento em que este participa. Esta relação pode definir-se informalmente nos seguintes termos:
A envolve B
se
A é um evento ou situação
B é uma entidade
e
A implica tipicamente B
Neste caso, por exemplo, agrafar implica tipicamente agrafo. Logo agrafar envolve agrafo. Esta relação é inversa da relação está envolvido em pelo que se agrafar envolve agrafo, então agrafo está envolvido em agrafar.
[voltar à tabela]
x está implicado como agente em
A relação está implicado como agente em é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um participante com a função de agente e o evento em que este participa. Esta relação pode definir-se informalmente nos seguintes termos:
A está implicado como agente em B
se
A é uma entidade
B é um evento ou situação
e
A é aquele que tipicamente realiza B
Neste caso, por exemplo, cozinheiro é aquele que tipicamente cozinha. Logo cozinheiro está implicado como agente em cozinhar. Esta relação é inversa da relação implica como agente pelo que se cozinheiro está implicado como agente em cozinhar, então cozinhar implica como agente cozinheiro (mas não necessariamente).
[voltar à tabela]
x implica como agente
A relação implica como agente é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um participante com a função de agente e o evento em que este participa. Esta relação pode definir-se informalmente nos seguintes termos:
A implica como agente B
se
A é um evento ou situação
B é uma entidade
e
A é tipicamente realizado por B
Neste caso, por exemplo, cozinhar é tipicamente realizado por cozinheiro. Logo cozinhar implica como agente cozinheiro (mas não necessariamente). Esta relação é inversa da relação está implicado como agente pelo que se cozinhar implica como agente cozinheiro (mas não necessariamente), então cozinheiro está implicado como agente em cozinhar.
[voltar à tabela]
x é instrumento para
A relação é instrumento para é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um participante com a função de instrumento e o evento em que este participa. Esta relação pode definir-se informalmente nos seguintes termos:
A é instrumento para B
se
A é uma entidade
B é um evento ou situação
e
A é o instrumento utilizado para B
Neste caso, por exemplo, faca é o instrumento utilizado para cortar. Logo faca é instrumento para cortar. Esta relação é inversa da relação envolve como instrumento pelo que se faca é instrumento para cortar, então cortar envolve como instrumento faca (mas não necessariamente).
[voltar à tabela]
x envolve como instrumento
A relação envolve como instrumento é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um participante com a função de instrumento e o evento em que este participa. Esta relação pode definir-se informalmente nos seguintes termos:
A envolve como instrumento B
se
A é um evento ou situação
B é uma entidade
e
A realiza-se através da utilização de B
Neste caso, por exemplo, cortar pode realizar-se através da utilização de faca. Logo cortar envolve como instrumento faca (mas não necessariamente). Esta relação é inversa da relação é instrumento para pelo que se cortar envolve como instrumento faca (mas não necessariamente), então faca é instrumento para cortar.
[voltar à tabela]
x está implicado como objecto em
A relação está implicado como objecto em é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um participante com a função de paciente e o evento em que este participa. Esta relação pode definir-se informalmente nos seguintes termos:
A está implicado como objecto em B
se
A é uma entidade
B é um evento ou situação
e
A é aquele que está sujeito à realização de B
Neste caso, por exemplo, refrigerante está sujeito à realização de beber. Logo refrigerante está implicado como objecto em beber. Esta relação é inversa da relação implica como objecto pelo que se refrigerante está implicado como objecto em beber, então beber implica como objecto refrigerante (mas não necessariamente).
[voltar à tabela]
x implica como objecto
A relação implica como objecto é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um participante com a função de paciente e o evento em que este participa. Esta relação pode definir-se informalmente nos seguintes termos:
A implica como objecto B
se
A é um evento ou situação
B é uma entidade
e
A é realizado afectando B
Neste caso, por exemplo, beber pode afectar refrigerante. Logo beber implica como objecto refrigerante (mas não necessariamente). Esta relação é inversa da relação está implicado como objecto em pelo que se beber implica como objecto refrigerante (mas não necessariamente), então refrigerante está implicado como objecto em beber.
[voltar à tabela]
x é lugar para
A relação é lugar para é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um espaço e o evento que nele tipicamente se realiza. Esta relação pode definir-se informalmente nos seguintes termos:
A é lugar para B
se
A é uma entidade
B é um evento ou situação
e
A é onde acontece B
Neste caso, por exemplo, escola é onde geralmente acontece ensinar. Logo escola é lugar para ensinar. Esta relação é inversa da relação tem lugar em pelo que se escola é lugar para ensinar, então ensinar tem lugar em escola (mas não necessariamente).
[voltar à tabela]
x tem lugar em
A relação tem lugar em é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um espaço e o evento que nele tipicamente se realiza. Esta relação pode definir-se informalmente nos seguintes termos:
A tem lugar em B
se
A é um evento ou situação
B é uma entidade
e
A acontece em B
Neste caso, por exemplo, ensinar acontece tipicamente em escola. Logo ensinar tem lugar em escola (mas não necessariamente). Esta relação é inversa da relação tem lugar em pelo que se ensinar tem lugar em escola (mas não necessariamente), então escola é lugar para ensinar.
[voltar à tabela]
x é meio físico para
A relação é meio físico para é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um meio e o evento que nele tipicamente se realiza. Esta relação pode definir-se informalmente nos seguintes termos:
A é meio físico para B
se
A é uma entidade
B é um evento ou situação
e
A é o meio onde acontece B
Neste caso, por exemplo, água é o meio onde pode acontecer nadar. Logo água é meio físico para nadar (mas não necessariamente). Esta relação é inversa da relação tem como meio físico pelo que se água é meio físico para nadar (mas não necessariamente), então nadar tem como meio físico água.
[voltar à tabela]
x tem como meio físico
A relação tem como meio físico é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um meio e o evento que nele tipicamente se realiza. Esta relação pode definir-se informalmente nos seguintes termos:
A tem como meio físico B
se
A é um evento ou situação
B é uma entidade
e
A acontece através B
Neste caso, por exemplo, nadar acontece através da água. Logo nadar tem como meio físico água. Esta relação é inversa da relação é meio físico para pelo que se nadar tem como meio físico água, então água é meio físico para nadar (mas não necessariamente).
[voltar à tabela]
x é ponto de origem de
A relação é ponto de origem para é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um ponto e o evento que nele tem origem. Esta relação pode definir-se informalmente nos seguintes termos:
A é ponto de origem de B
se
A é uma entidade
B é um evento ou situação
e
A é o ponto onde se inicia B
Neste caso, por exemplo, avião é o ponto onde se inicia desembarcar. Logo avião é ponto de origem de desembarcar. Esta relação é inversa da relação tem como ponto de origem pelo que se avião é ponto de origem de desembarcar, então desembarcar tem como ponto de origem avião.
[voltar à tabela]
x tem como ponto de origem
A relação tem como ponto de origem é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um ponto e o evento que nele tem origem. Esta relação pode definir-se informalmente nos seguintes termos:
A tem como ponto de origem B
se
A é um evento ou situação
B é uma entidade
e
A inicia-se no ponto B
Neste caso, por exemplo, desembarcar inicia-se em avião. Logo desembarcar tem como ponto de origem avião. Esta relação é inversa da relação é ponto de origem de pelo que se desembarcar tem como ponto de origem avião, então avião é ponto de origem de desembarcar.
[voltar à tabela]
x é ponto de destino/chegada de
A relação é ponto de destino/chegada para é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um ponto e o evento que nele culmina. Esta relação pode definir-se informalmente nos seguintes termos:
A é ponto de destino/chegada de B
se
A é uma entidade
B é um evento ou situação
e
A é o ponto onde termina B
Neste caso, por exemplo, avião é o ponto onde termina embarcar. Logo avião é ponto de destino/chegada de embarcar. Esta relação é inversa da relação tem como ponto de destino/chegada pelo que se avião é ponto de destino/chegada de embarcar, então embarcar tem como ponto de destino/chegada avião.
[voltar à tabela]
x tem como ponto de destino/chegada
A relação tem como ponto de destino/chegada é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um ponto e o evento que nele culmina. Esta relação pode definir-se informalmente nos seguintes termos:
A tem como ponto de destino/chegada B
se
A é um evento ou situação
B é uma entidade
e
A termina no ponto B
Neste caso, por exemplo, embarcar termina em avião. Logo embarcar tem como ponto de destino/chegada avião. Esta relação é inversa da relação é ponto de destino/chegada de pelo que se embarcar tem como ponto de destino/chegada avião, então avião é ponto de destino/chegada de embarcar.
[voltar à tabela]
x resulta de
A relação resulta de é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um participante com a função de resultado e o evento que lhe dá origem. Esta relação pode definir-se informalmente nos seguintes termos:
A resulta de B
se
A é uma entidade
B é um evento ou situação
e
A passa a existir como resultado de B
Neste caso, por exemplo, borboleta passa a existir como resultado de metamorfose. Logo borboleta resulta de metamorfose. Esta relação é inversa da relação tem como resultado pelo que se borboleta resulta de metamorfose, então metamorfose tem como resultado borboleta (mas não necessariamente).
[voltar à tabela]
x tem como resultado
A relação tem como resultado é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, e que permite ligar um participante com a função de resultado e o evento que lhe dá origem. Esta relação pode definir-se informalmente nos seguintes termos:
A tem como resultado B
se
A é um evento ou situação
B é uma entidade
e
A dá origem a B
Neste caso, por exemplo, metamorfose pode dar origem a borboleta. Logo metamorfose tem como resultado borboleta (mas não necessariamente). Esta relação é inversa da relação resulta de pelo que se metamorfose tem como resultado borboleta (mas não necessariamente), então borboleta resulta de metamorfose.
[voltar à tabela]
x causa
A relação causa permite ligar pares de eventos que evidenciem uma relação causal. Estes eventos podem ser temporalmente disjuntos, sobrepostos ou coextensos, ou seja, podem não ter em comum qualquer ponto no eixo do tempo, partilhar alguns pontos no eixo do tempo ou ter todos os pontos no eixo do tempo em comum. A relação causa é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, podendo definir-se informalmente nos seguintes termos:
A causa B
se
A e B são ambos eventos ou situações
e
A tem como consequência B
Por exemplo, ressuscitar tem como consequência viver. Logo ressuscitar causa viver. Esta relação é inversa da relação tem como causa pelo que se ressuscitar causa viver, então viver tem como causa ressuscitar (mas não necessariamente).
[voltar à tabela]
x tem como causa
A relação tem como causa permite ligar pares de eventos que evidenciem uma relação causal. Estes eventos podem ser temporalmente disjuntos, sobrepostos ou coextensos, ou seja, podem não ter em comum qualquer ponto no eixo do tempo, partilhar alguns pontos no eixo do tempo ou ter todos os pontos no eixo do tempo em comum. A relação tem como causa é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, podendo definir-se informalmente nos seguintes termos:
A tem como causa B
se
A e B são ambos eventos ou situações
e
A acontece na sequência de B
Por exemplo, viver pode acontecer na sequência de ressuscitar. Logo viver tem como causa ressuscitar (mas não necessariamente). Esta relação é inversa da relação causa pelo que se viver tem como causa ressuscitar (mas não necessariamente), então ressuscitar causa viver.
[voltar à tabela]
x tem como subevento
A relação tem como subevento permite exprimir uma relação do tipo todo/parte entre eventos e corresponde a uma relação de inclusão entre pares de eventos. A relação tem como subevento é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, podendo definir-se informalmente nos seguintes termos:
A tem como subevento B
se
A e B são ambos eventos ou situações
A é um evento complexo
e
A consiste em vários eventos entre os quais B
Sempre que A, então B
Por exemplo, respirar consiste em vários eventos entre os quais inspirar e sempre que se respira, inspira-se. Logo respirar tem como subevento inspirar. Esta relação é inversa da relação é subevento de pelo que se respirar tem como subevento inspirar, então inspirar é subevento de respirar.
[voltar à tabela]
x é subevento de
A relação é subevento de permite exprimir uma relação do tipo parte/todo entre eventos e corresponde a uma relação de inclusão entre pares de eventos. A relação é subevento de é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, podendo definir-se informalmente nos seguintes termos:
A é subevento de B
se
A e B são ambos eventos ou situações
B é um evento complexo
e
A acontece como parte de B
Sempre que B, então A
Por exemplo, inspirar acontece como parte de respirar e sempre que se respira, inspira-se. Logo inspirar é subevento de respirar. Esta relação é inversa da relação tem como subevento pelo que se inspirar é subevento de respirar, então respirar tem como subevento inspirar.
[voltar à tabela]
x é o modo de ocorrência de
Muitos subtipos verbais são definidos por incorporação do modo como um determinado evento se desenvolve. Não sendo a única forma de especificação de hipónimos eventivos, é uma das mais salientes, pelo que existe uma relação que permite explicitar o modo que caracteriza um dado evento e que o distingue dos seus co-hipónimos: a relação é o modo de ocorrência de. A relação é o modo de ocorrência de é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, podendo definir-se informalmente nos seguintes termos:
A é o modo de ocorrência de B
se
A é um advérbio
B e C são ambos eventos ou situações
e
B é um subtipo (hipónimo) de C
B distingue-se de C por ocorrer do modo A
Por exemplo, sorver é um subtipo de comer, sorver distingue-se de comer por ocorrer ruidosamente. Logo ruidosamente é o modo de ocorrência de sorver (mas não necessariamente). Esta relação é inversa da relação tem como modo de ocorrência pelo que se ruidosamente é o modo de ocorrência de sorver (mas não necessariamente), então sorver tem ruidosamente como modo de ocorrência.
[voltar à tabela]
x tem como modo de ocorrência
Muitos subtipos verbais são definidos por incorporação do modo como um determinado evento se desenvolve. Não sendo a única forma de especificação de hipónimos eventivos, é uma das mais salientes, pelo que existe uma relação que permite explicitar o modo que caracteriza um dado evento e que o distingue dos seus co-hipónimos: a relação tem como modo de ocorrência. A relação tem como modo de ocorrência é uma relação assimétrica, que pode ser facultativa em qualquer dos dois sentidos, podendo definir-se informalmente nos seguintes termos:
A tem como modo de ocorrência B
se
A e C são ambos eventos ou situações
B é um advérbio
e
A é um subtipo (hipónimo) de C
A distingue-se de C por ocorrer do modo B
Por exemplo, sorver é um subtipo de comer, sorver distingue-se de comer por ocorrer ruidosamente. Logo sorver tem ruidosamente como modo de ocorrência. Esta relação é inversa da relação é o modo de ocorrência de pelo que se sorver tem ruidosamente como modo de ocorrência, então ruidosamente é o modo de ocorrência de sorver (mas não necessariamente).
[voltar à tabela]
|
