|
 |
|
|
|
|
Drawing according to the illustration presented by Pedro Nunes, in De Crepusculis, which accompanied the description of the nonius.
|
|
|
|
The nonius concept
We are certain that when Pedro Nunes (1502-1577) concerned himself with this problem he was not aware of Levi’s work for although it had been translated into Latin, being a manuscript it did not have a widespread dissemination. And the same applies to Digges’ work which, although printed, is subsequent to his invention. In fact, had this happened, it may have discouraged our illustrious sage for his concept of nonius has the same objective as the diagonal scale.
The nonius appears in the work De Crepusculis, published in 1542. In the second part of this work, postulate number three reads as follows: “Construct an instrument that is very appropriate for observing the heavenly bodies and which can be used to accurately determine the respective altitudes”.
The idea which stimulated our cosmographer, described in his work titled De arte atque ratione navigandi, was a passage from the Almagesto (page 9 of the 1515 edition), in which Ptolemy considers that the value of the meridian arc between the two tropics corresponds to the faction 11/83 of the circumference. He also said that the limb of the instrument used for this measurement should be divided into degrees and that each degree should be divided into parts of the degree, without fixing their number.
Knowing that at the time of the wise man from Alexandria there were no such instruments that made such precision possible, and perhaps being inspired by the proportion between these two integers, Pedro Nunes developed the postulate referred to above, inventing what became known as the nonius.
|
 |
|
|
|
(click on the picture above to see an enlarged version)
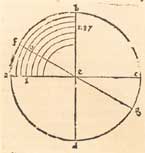
Diagram in which the positions of the nonius, between 37 and 38º, referred in Fig. 7, are shown graphically. Following the example presented in the text, if we wish to measure an angle of 37º 23’ (where the alidade is placed), we find that the 27th position of the nonius is the closest to this value in the scale divided into 65 positions. The reading would have had an error of .08’, which in this case is less than the average error of 2.13 minutes indicted in the text.
|
|
|
|
 |
|
|
|
Positions of the nonius between 37 and 38º, distributed over its various scales. It was seen that some positions are repeated in different scales. The column on the left, between brackets, indicates first the position on the scale, followed by the number of divisions in which this scale was divided. The column on the right gives us the angular value of each position or positions when these coincide.
|
|
|
In an astrolabe graduated from 0 to 90 degrees, 44 additional concentric scales were built, divided into 89, 88, 87, etc., successively, the last being divided into 46 equal parts. In this way, on measuring a certain angle, which does not correspond to an exact number of degrees, it is highly likely that its value fall precisely on, or very close to, a division of the referred scales. Let us suppose that we wished to measure an angle of 37 degrees and 23 minutes. If we look at the table opposite, where all of the positions of the nonius between 37 and 38 degrees have been included, the 27th position of scale 65 of the divisions measures 37 degrees and 23.08 minutes, which makes it possible to obtain a readying with a deviation of only 8 hundredths of a minute. In order to have a clearer idea of what happens in the above-mentioned sector, we made a drawing, which is not according to scale, in which we can evaluate the positions of the nonius contained in it.
n the example presented, the deviation was 8 hundredths. Such an approximation is not always possible since the average deviation between the two positions is greater. In fact, if we divide the quadrant by the number of unrepeated positions of the nonius, we realise that the average deviation is slightly more than 2 minutes of arc.
Nevertheless, this average deviation is deceiving, given that the distribution of the nonius’ positions is very irregular. Despite having calculated all of its positions, as referred above, we did not realise that there are a number of sectors, which can go as far as 30’, which do not contain a single position. This discovery was made by Jean Widemann, who calculated the distance between all the positions of the nonius, with very surprising results.
Some of the most significant voids are listed below:
between 44º 30’ and 45º 30’, the only graduation that exists is 45º;
between 29º 40’ and 30º 20’, only position 30º exists and, as in the nonius there is a strict symmetry in relation to the 45º, also between 59º 40’ and 60º 20’, only position 60º appears;
between 22º 15’ and 22º 45’ and between 67º 15’ and 67º 45’, only positions 22º 30’ and 67º 30’, respectively, can be found.
The examples continue, yet the distances naturally become smaller. Without a doubt, the nonius would be extremely useful (the irregular distribution of its positions was unknown at the time) when integrated in an astrolabe, for this was the instrument chosen by Nunes for the application of his invention. Nevertheless, the marking of the 45 scales (we are including the main scale, from zero to 90º) was extremely difficult work for that time period due to the fact that there were no geometrical processes to perform a correct division. Moreover, the question of space also had to be taken into account. In fact, if marking a planispheric or nautical disc astrolabe (with a diameter of 20 or 25 centimetres) already had its limitations, this became impossible in the nautical wheel astrolabe.
In our journey along this fascinating path, we will try to discover the dissemination of this invention and which instruments used it.
In this regard, in Portugal a description of the nonius can be found in Arte de Navegar, of 1596, which the priest Francisco da Costa calls “quadrant of quadrants”, with not even the slightest reference to its author.
Before Francisco da Costa, another Portuguese, João Baptista Lavanha, presented a detailed description of the nonius in his Tratado del Arte de Navegar, of 1588, written in Castilian, also failing to make any reference to the sage from Alcácer do Sal.
We did not find a single copy of an instrument incorporating the nonius that may have existed in our country, or even any account of it. Nevertheless, in 1818 Francisco Stockler pointed out that all doubts about the nonius could be dispelled “if the instruments which Pedro Nunes used, and which to a large extent were constructed due to him, still existed. As fate would have it, however, this precious deposit fell into the hands of the religious Benedictine monks of the college which this monastic order has in Coimbra. On being informed that a portion of yellow metal was needed to make some gargoyles, the abbot who ruled this college when the bars of the churchyard were made, under the belief that these astronomical instruments, of which the monks made no use, were absolutely useless devices, converted them into the aforementioned ornaments. And such was their destiny, victims of an ignorant economy, scientific monuments, precious for their antiquity and respectful of the genius who invented some, perfected others and wielding all of them with exceptional skill”. Stockler explains that this was a well-known “anecdote” in Coimbra when he graduated from this university and that it was “transmitted by a very curious, solemn and veracious person”.
We admit that it is perfectly possible that this could have happened, as unfortunately this is not the only case of destruction of scientific patrimony in our country.
There is, however, no documental evidence to support Stockler’s statement. Even the bars containing the aforementioned gargoyles were demolished along with the church many years ago. Nevertheless, even if this episode did in fact occur, there is nothing to prove that Pedro Nunes did have instruments that incorporated his nonius. Firstly because, as mentioned above, we are unaware of any account in this regard, and secondly, because the division and marking of scales on a nonius was arduous work, requiring artificers of great skill which did not exist in Portugal at that time.
The same cannot be said of other countries, however. During the second half of the sixteenth century, in various cities like Augsburg, Nuremberg and Antwerp, famous artists like Christoph Schissler, Tobias Volckmer and Gemma Frisius, to mention just a few, left us instruments of extremely high quality. The reason for this is because, these artificers, besides having a perfect notion of the function of these instruments, knew their manufacturing processes so well and used them with such skill, that they left us with such elaborate works that even today cause widespread admiration.
Nothing of this ever happened in our country. Besides the nautical astrolabe, which was developed and manufactured by the Portuguese, albeit using elementary technology, and which at the time and beyond any doubt was the most prestigious instrument for measuring altitudes, there is no recollection of a planispheric astrolabe, a vital instrument for the cosmographers of yore, ever having been made in Portugal. Of these beautiful instruments, over 1300 reached our days, for the list that refers this number dates back to 1955 and since then many others have been catalogued. Of these beautiful instruments, over 1300 reached our days, for the list that refers this number dates back to 1955 and since then many others have been catalogued.
|
|




